一，AI工作原理

我们日常生活中接触的大语言模型(LLM),简单来讲就是所谓的AI.它的工作原理其实非常简单,用户输入一段文字之后会得到一个输出的文字内容.输入到输出的这种模式可以想起数学中的一个概念叫函数,说白了LLM就是一个大型的函数套娃系统.

一般我们所学的函数结果是固定的,比如我给x提供一个值那么必然会有个对应的y输出.这种固定性显然跟我们需要的AI不符合,跟AI的每一次聊天都是不同的,不会因为输入内容的相同而输出同样的内容.关于这种随机性和准确性是怎么搞出来的,下面会从最基础的概念到深层概念递进方式介绍这些概念.

二，权重

权重是指一个数据对另一个数据的重要程度,也就是相互关联性有多强的标志.下面举一个例子:

我在路上看见了一只猫,它很可爱.

在上面这个句子当中,对比一下”我”和”可爱”的关系,再对比一下”猫”和”它”的关系.显然”它”本身指的就是”猫”所以这两之间的关联性很强,也就是权重最高.”我”和”可爱”这两个词的关联性就没有那么强了权重也比较低.这就是权重的概念.

最开始人们引入了重要性的概念,也就是把所有输入进行求和,但是这显然有个弊端,无法知道输入的第一个字和下个字之前的关联:
$$
z = x_1 + x_2 + \cdots + x_n = \sum_{i=1}^{n} x_i
$$
这样的合并方式导致所有输入的重要性都是同等存在的,无法确认字和字之前的重要性了,所以就引入了一个新的概念叫权重.
$$
z = \sum_{i=1}^{n} (x_i \cdot w_i)
$$
现在w_i作为权重可以控制对输入x_i的影响力了.举个例子比如我们的输入有三个声音分别是x_1,x_2,x_3.这三个声音当中x_2是噪音,剩下的是正确声音.按照以上公式进行计算时由于x_1是正确的所以权重w_1会调大一点,到了x_2发现是噪音为了不影响最终结果会把w_2调小一点甚至调成负的.通过控制w_i来对生成结果进行控制.

这就是ai的”学习“过程,通过不断的控制权重w_i来输出最接近真实答案的过程.

三，激活函数

上一部分我们升级了函数通过权重进行控制输出内容,为了达到更好的控制效果下一步我们加入一个可以调节的变量:

$$
z = \left( \sum_{i=1}^{n} (x_i \cdot w_i) \right) + b
$$
这里所加的b变量叫做偏置(Bias),简化的公式就变成了:

输出 = (权重求和) + 偏置

这个偏置b是独立于所有输入内容,因此可以调整函数输出,使整体上下移动.这个完整的式子全部当中一个整体就成为了激活函数:
$$
y = f(z) = f\left(\left(\sum_{i=1}^{n} (x_i \cdot w_i)\right) + b\right)
$$
相当于这里的z通过一个决策函数来生成最终的输出,以下是简化公式:

最终输出 = 激活函数( 加权和 + 偏置 )

因此可以得出激活函数就相当于是个权重之和加上了一个偏置的函数罢了.

四，神经元和神经网

一听到神经元就能想起生物学上的组成神经系统的细胞,ai领域的神经元概念跟这个大差不差,下面是生物学上面的神经元概念图:

从这个图可以看出很多神经元细胞相互连接生成了一个复杂的网状结构,那ai领域的神经元是不是也是这样的网状结构咱们来探索一下.

既然我们知道了激活函数,那么也就知道了神经元的输出就是激活函数的值:

神经元输出 = 激活函数( 加权和 + 偏置 )

知道了神经元,接下来解释一下神经网是怎么构成的,我们这里把一个神经元想象成一个乐高积木,把很多乐高积木连在一起排成一排并列(左右排序)的形式.这一排就代表一层:

层₁ = [神经元₁, 神经元₂, 神经元₃, ...]
层₂ = [神经元₁, 神经元₂, 神经元₃, ...]
层₃ = [神经元₁, 神经元₂, 神经元₃, ...]
.............

把这种层称为神经元层,现在把每一排的乐高积木上下叠加在一起组成了网络:

输入 -> 层₁ -> 层₂ -> 层₃ -> ... -> 输出

这种把多个层叠加在一起形成的网络结构就成为神经网.

五，输入层,输出层,隐藏层

在组成的神经网当中丢给ai的内容叫做输入层.输入层可以是任何形式的文字,因为函数计算的是数字计算机认识的也是数字,所以不管是音频,视频,图片,文字等各种形式的资源全部都得转换成数字的形式丢给这个神经网.

输入层进入的数据会经过神经元层当中的神经元的计算到达下一个层,这过程当中会经过很多个层最后再到达输出层(层的多少取决于模型的复杂程度),这种在中间我们看不到的层叫做隐藏层.

经过多个隐藏层最后到我们看到的输出内容,最后经过的这个层叫做输出层.

六，损失函数

我们已经完成了一个完整的神经网,这个神经网会根据输入经过一系列计算得出输出结果.但是我们怎么知道这个输出结果是否正确.比如我们输入给了一个车的照片但是输出内容中显示这个是动物的概率有多大.为了知道模型训练的好坏就诞生了这个损失函数的概念.下面我们来看一张图: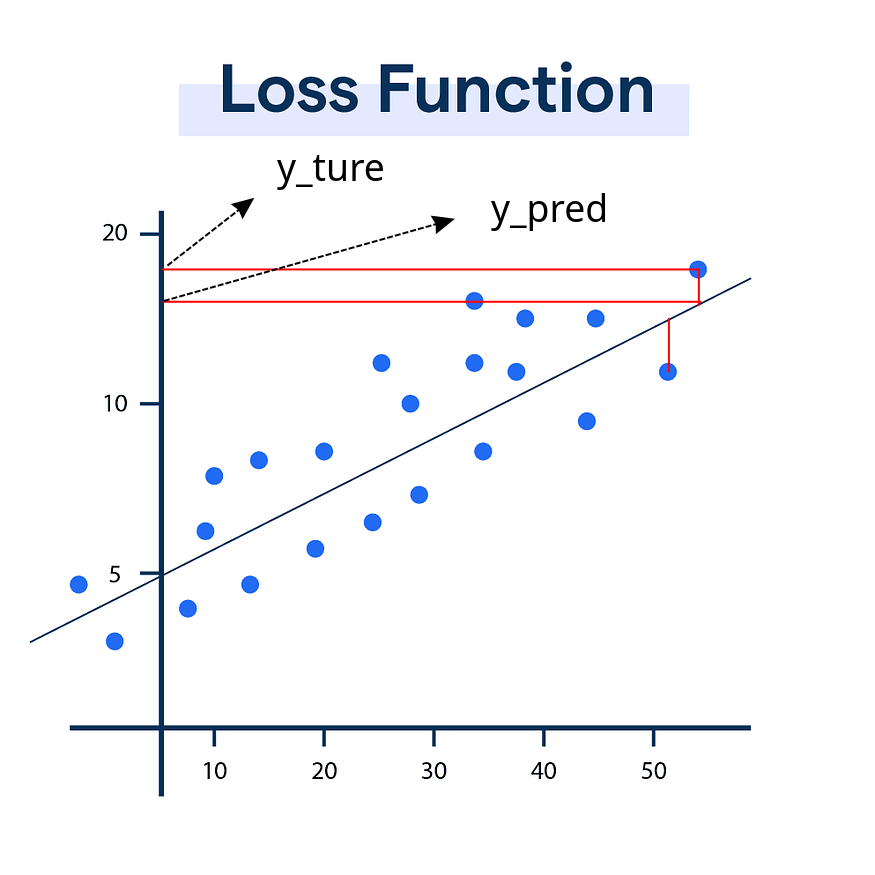

看到照片不要被吓一跳,其实要讲的内容很简单.在这个图当中蓝色的点代表我们的训练样本也就是丢给ai让其学习的资料.黑色的线代表ai从这个样本当中学习得到的规律(实际上这个函数不是线性的,这里为了方便展示举例的).

我来举个例子,我们给ai丢了大量的公司年收入数据,每个蓝色的点代表每年的年收入,然后ai试图学习找出这个年收入的规律就画出了这么一条线用来预测未来的年收入.从这条线上面得到的数据都是一个预测值 y_pred .而实际的年收入就是真实值y_true.那这个真实收入和预测收入之间的差叫做误差.

带着这些知识看图应该轻轻松松就能理解,下面把上面所说的结合成公式来看一下:
$$
Loss = |y_{\text{true}} - y_{\text{pred}}|
$$
绝对值在数学当中每次都让人特别头疼,所以为了方便我们去掉绝对值换成更加简单的平方,改成平方有两个好处一个是我们不关心误差是大了还是小了,另一个是可以容忍小幅度的误差比如2的平方是4,但绝不能容忍大幅度误差比如10的平方是100.这样就能避免犯很大的错误了.

接下来就对所有误差进行求和再求平均操作,这样就得到了最终的损失函数:
$$
Loss (MSE) = \frac{1}{n} \sum_{i=1}^{n} (y_{\text{true}, i} - y_{\text{pred}, i})^2
$$
损失函数得出的就是损失(Loss),我们整个训练的目标就很明确了,通过不断的调整神经元(激活函数)当中的权重和偏置让这个损失值变得最小.

七，正向传播和反向传播

结合上面所学的知识我们重新疏理一下整个流程,首先用户进行输入,第一层拿到输入层的数据之后调整权重和偏置再把得出的结果传递给下一层,下一层根据上一层给的数据调整自己的权重和偏置再传递给下一层以此类推最后到达输出层.这种从输入层到输出层的参数调整过程就成为正向传播.

最终拿到输出层的数据之后跟我们原来训练用的正确数据进行对比,这就好比学生作答老师对比正确答案看看学生的答案跟正确答案到底偏离了多少.然后给出一个分数这个分数就是我们前面所说的损失值(Loss),分数越高就说明错的越离谱.咱们就不讨论损失值低的情况,那损失值高了怎么办?

损失值高得找出是什么原因导致的,从最后一层往前推算出神经网络当中的每一个参数(权重和偏置)为这次的错误有多大的责任,然后告诉他要把适当的往正确的方向进行调整.这就是”学习”的核心,而这整个往后推算的过程叫反向传播.

八，梯度

1.梯度的概念

我们来举一个经典的例子,你要去爬山,上山最快的指向山顶的那个方向就是梯度,正向传播过程中会出现这个梯度.这个山脉的地形相当于是个损失函数,山的高度就是损失值.我们的位置代表了模型当中所有参数(权重,偏置)的取值.我们的目标就是要下山找到山的最低位置(损失值最小的点).

2.梯度下降

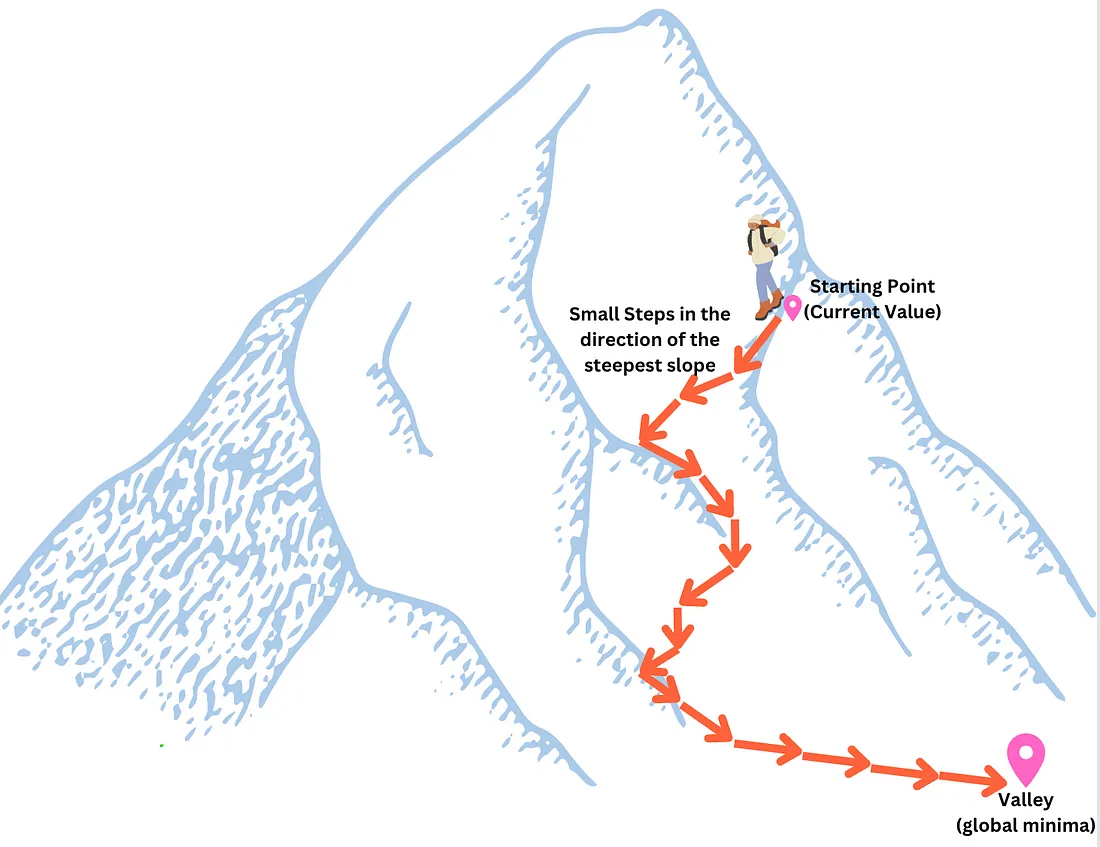
要下山时我们的眼睛被人蒙上了,蒙着眼睛下山应该怎么做?

按正常逻辑来讲肯定要用脚试探性的感受一下哪个方向是对下山来说是陡峭的,朝着这个陡峭的方向小步小步的走最终肯定能走到山地.那我们这整个蒙眼下山的过程就是梯度下降.

通过反向传播,计算出损失函数对于每一个参数的梯度,这个梯度说白了就是如果我稍微调整这个权重w,损失函数就会上升的最快.梯度不停的下降损失值也会不停的下降.下面是梯度下降的简化公式:

新权重 = 旧权重 - 梯度

通过数学公式表达:
$$
w_{\text{new}} = w_{\text{old}} - \nabla L
$$
在数学当中我们把梯度标记为∇L.

3.梯度爆炸

在反向传播过程当中,梯度的计算就是从后往前的计算过程,计算过程极其复杂逐层相乘.万一算出来是个超大的数字,经过多次相乘会变成一个天文数字,这种情况就是梯度爆炸.层数越多,相乘的次数就越多,爆炸的风险就会变大.

那梯度爆炸的后果是什么权重的数值会变得无穷大最终计算出的效果也是特别糟糕,所有之前训练好的知识也会被摧毁导致模型完全不可用状态.

九，学习率

1.概念介绍

我们又回到下山的例子当中,假如我们是个巨人,一跨步就能走的很远.那我们很有可能跨一大步就跨过了山地直接到了另一个山上面.还有可能当前所在山比之前还高,我们又跨回去反复找山地,但是永远都达不到山的最低点.
训练当中损失函数就来回震荡,甚至可能变成不是数字的状态(NaN,Not a Number)导致训练失败.

假如我们是个蚂蚁,每一步跨的都特别小,最终肯定能走到山地,但是这个过程极其的漫长.
训练当中损失函数会下降的特别慢,训练耗费巨大的资源和时间.

上面两个例子当中所说的步子指的是学习率,在数学当中我们把学习率标记为η.

在梯度下降的过程当中,参数是通过梯度来变化的,那这个变化的大小就是学习率来定义,梯度下降的更新公式就变成了:

新权重 = 旧权重 − 学习率 × 梯度

通过数学公式表达:
$$
w_{\text{new}} = w_{\text{old}} - \eta \cdot \nabla L
$$

2.举例说明

下面会举例详细的学习步骤:
我们举一个最简单不带激活函数和偏置的神经元例子:
$$
y_{\text{pred}} = w * x
$$
我们的训练数据是x = 2时对应的答案y = 10,因为模型刚开始什么都不知道我们把权重设为w = 3.

(1)正向传播 : 模型用当前的权重进行预测

$$
y_{\text{pred}} = w * x = 3 * 2 = 6
$$

(2)计算损失

$$
Loss = (y_{\text{true}} - y_{\text{pred}})^2 = (10−6) ^2=4 ^2=16
$$

当前函数的损失值为16.

(3)反向传播

通过算法计算出损失对权重w的梯度是多少:
$$
\frac{\partial L}{\partial w} = 2(y_{\text{true}} - wx)(-x) = 2(10-6)(-2) = -16
$$
得出的数是-16说明当前的方向是”负向”的,为了减少损失我们肯定要增加权重w的值.

(4)使用学习率来更新权重

现在代入更新参数的公式:
$$
w_{\text{new}} = w_{\text{old}} - \eta \cdot \frac{\partial L}{\partial w} = 3 - \eta \cdot (-16)
$$
下面通过调整学习率的大小看看成果:

• η = 0.01 比较好一点的值
  $$
  w_{\text{new}} =3−0.01⋅(−16)=3−(−0.16)=3.16
  $$
  梯度要我们增加权重w的值,学习率控制了一点点,权重就从3变成了3.16,正确答案是5.已经在逐步接近真实答案了.

• η = 0.1 比较大的值
  $$
  w_{\text{new}} = 3−0.1⋅(−16)=3−(−1.6)=4.6
  $$
  现在权重从3直接变成了4.6,虽然这个值非常接近真实值,但是也有可能步子太大跨过正确值.

• η = 0.2 很大且危险的值
  $$
  w_{\text{new}} = 3−0.2⋅(−16)=3−(−3.2)=6.2
  $$
  现在权重直接跳到了6.2,已经越过真实答案,权重比之前更差了.这个就成为过冲(Overshooting).

• η = 0.0001 一个特别小的值
  $$
  w_{\text{new}} = 3−0.0001⋅(−16)=3−(−0.0016)=3.0016
  $$
  迈出了一小步,按照正确方向控制了,但是变化太小,需要成千上万次的这种更新才能达到正确的值.

十，拟合

假设现在我们有很多数据样本,模型经过不停的训练会得出一个接近真实函数的曲线.要是得出的不是曲线而是一个直线只能正确输出某一部分值的话,这就说明模型欠拟合.要是训练出来的模型函数非常接近真实函数那么这就是拟合良好.

要是训练出来的模型函数可以准确计算出所有训练中的数据,但是无法正确计算出训练数据集之外的数据这就说明是过拟合.

看下面这张图就一目了然了:

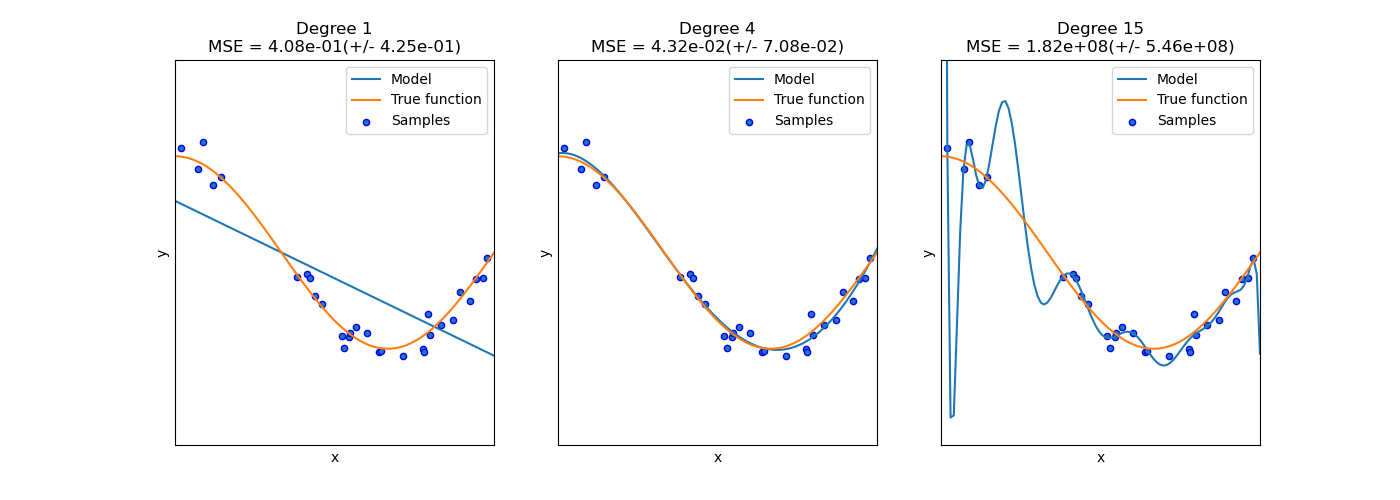
• 第一张图橙色的曲线代表是真实的函数曲线,蓝色的直线代表模型训练完之后的函数,这种状态下模型只有在一部分情况下能得出正常的答案,但在大部分情况下结果跟实际偏差太大.这种情况就是典型的欠拟合
• 第二张图当中模型的函数跟真实的函数几乎是贴近的,这种情况下模型的函数是最佳的,也成为拟合良好.
• 第三张图当中模型能准确的算出所有的训练数据,但是只要给的数据是训练数据集之外的那么模型就出现很大的损失,这种情况就是典型的过拟合状态.

十一，泛化能力

模型在自己训练的数据上的得分表现特别好,但是在没见过的数据上的表现特别差的情况,也就是刚刚提到的过拟合状态.模型的这种情况称为泛化能力差.

泛化能力所指的就是模型在自己没有见过的数据集上的表现能力.为了提高模型的泛化能力可以增大数据集,调整学习率等各种手段来防止过拟合.

十二，正则化

我们已经知道了过拟合的模型在新数据上的表现能力很差,一个过拟合的模型在数学上通常是由于它内部的权重w变得很大,从上方的过拟合函数图就能发现函数的变化幅度很大.既然是由权重w过大导致的,那有没有办法让训练过程中的w一直保持小的状态呢?

当然有,人们想到了一个极其绝妙的办法来解决了这个过拟合的问题,那就是给损失函数加上一个所有权重的平方和,简化公式如下:

总损失 = 损失值 + 正则化惩罚项

1. L2正则化

目前应用最广泛的就是L2正则化,也被称为权重衰减.就是给损失值加上一个所有权重的平方和.这样即保证了模型梯度的正确下降也保证了过拟合的出现.下面来看看这个惩罚公式:
$$
\text{L2 惩罚项} = \lambda \sum_{i=1}^{n} w_i^2
$$
然后完整的损失函数就是:
$$
总损失=预测误差+ \lambda \sum_{i=1}^{n} w_i^2
$$
在L2正则化当中权重是平方的,所以一个很大的权重会导致惩罚变得很大,所以在训练时模型会尽可能的让权重缩小.还有一个特征是不会让权重变成0,及时是一个非常小的权重比如0.00001,平方之后权重变得极其微小.所以会无限接近0但是不会变成0.

2. L1正则化

L1正则化是一个更加强大的正则化技术,看惩罚公式就能知道它的强大之处了:
$$
\text{L2 惩罚项} = \lambda \sum_{i=1}^{n} |w_i|
$$
因为是绝对值之和而不是平方和,所以权重调整的过程当中可以变成0.权重变成0说明权重连接的这个神经元就被关闭了.所以不需要的特征都会被关闭,只保留那些最有用的特征.这就使得模型变得简单,变得更小.

一般来说L2正则化主要防止过拟合使权重普遍变小,L1正则化让部分权重变0,简化模型,筛选特征.

十三，鲁棒性

一个模型的所有数据都完好无损,泛化能力也很不错,能够正确的输出答案.但是我们的输入稍微加一点变化比如输入当中带点错别字,逻辑有问题的句子等.输出的结果还是正确的说明这个模型的鲁棒性很好,输出结果变得糟糕说明鲁棒性很差.

为了提高模型的鲁棒性,就在训练时给模型提供各种各样没有见过的数据,对于文字可以适当的把替换文字当中的同义词,删除某些单词,改变语序等.对于图片可以对图片进行不同程度的旋转,裁剪等